Spotvol Toolbox
by Till Sabel and Johannes Schmidt-Hieber (January, 2014|Download current version 1.1)
GENERAL
For given high-frequency financial data, the Spotvol Toolbox computes and plots the spot volatility (the volatility process over time) given high-frequency financial data. It is designed to deal with microstructure noise effects, and corrects for possible jumps in the (log)-price process (data).
Some facts about high-frequency data:
- On small scales (below five minutes sampling frequency), microstructure effects are present and need to be taken into account. SDE driven models without non-continuous noise component lead to inconsistent (much too large) estimates for the volatility.
- Due to external shocks such as macroeconomic announcements, jumps (and clusters of jumps) are present in financial data. They can and need to be filtered out.
- There are many specific models in order to describe the dynamics of asset prices and spot volatility (as for instance the Heston model). However, each of these models captures only some of the effects observed in empirical data. For a reliable reconstruction of volatility, it is therefore unavoidable to model the price process more generally by a semi-martingale, which especially implies that the spot volatility cannot be parametrized.
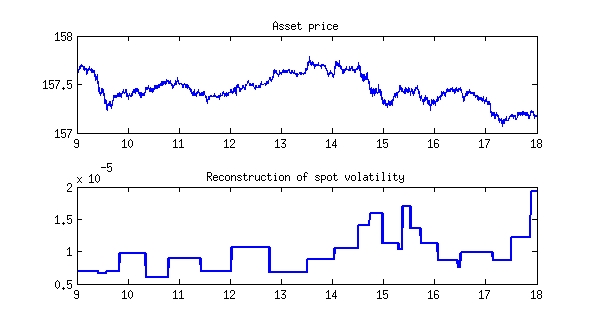
FEATURES OF THIS TOOLBOX
Spot volatility estimation:
- The procedure accounts for microstructure noise by a first pre-averaging step.
- The pre-averaging is optimized by a data-driven choice of the block length.
- The procedure corrects for various types of jumps in the data by applying jump-detection tests in combination with a data cleaning procedure.
- A wavelet expansion of the spot volatility is used.
- The wavelet coefficients are thresholded via SURE block thresholding.
Spot covolatility estimation:
- This is at the moment at a beta-level.
- The method requires synchronized high-frequency data as input.
REQUIREMENTS
- Matlab Wavelet Toolbox required
- Runs stable for Matlab Version 7.10.0.499 (R2010a)
TUTORIAL
As an introduction, run GUI.m in subdirectory "Examples" of the toolbox. Also see GUIhelp.txt there. For advanced use of the toolbox, run ASVE.m in subdirectory "Code" and see its internal manual.
DOWNLOAD & RELEASE INFORMATION
Current Release: Spotvol Toolbox 1.1 under the terms of the GNU General Public License, January 21st, 2014
Programmer: Till Sabel, Johannes Schmidt-Hieber
Send bug reports and further suggestions to: tsabel@uni-goettingen.de, schmidthieberaj@math.leidenuniv.nl
MAIN REFERENCE
FURTHER REFERENCES
Cai, T. and Zhou, H. (2009). A data-driven block thresholding approach to wavelet estimation. Ann. Stat. 37 569–595.
Cohen, A. (2003). Numerical Analysis of Wavelet Methods. Elsevier.
Hayashi, T. and Yoshida, N. (2005). On covariance estimation of non-synchronously observed diffusion processes. Bernoulli 11 359–379.
Hoffmann, M., Munk, A. and Schmidt-Hieber, J. (2012). Adaptive wavelet estimation of the diffusion coefficient under additive error measurements. Ann. Inst. H. Poincare Probab. Statist. 48(4) 1186–1216.
Jacod, J., Li, Y., Mykland, P. A., Podolskij, M. and Vetter, M. (2009). Microstructure noise in the continuous case: the pre-averaging approach. Stochastic Process. Appl. 119(7) 2249–2276.

